e是多少数值（e为什么和计算利息有关）

自然常数e是一个非常重要的无理数，它的存在很大程度上影响了我们的学习与生活。自然常数e为什么这么重要？

什么是自然常数e？

它的定义是

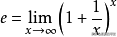
其数值约为：e ≈ 2.71828

为什么自然常数e和银行利息有关呢？

这里以一个银行存款的例子简单描述一下：

我们在银行存款是有利息的，而存款赚到的利息又可以继续和本金一起，赚取更多的利息。

当然，银行不是慈善家，它们结算利息的频率很低，要每一年甚至三年才结算一次，也就是说，在这一年或者三年的时间里，已经获得的利息并不能帮我们赚取更多利息。

下面考虑一种理想状况，也就是假定有这样一家银行，它一年的存款利率是100% (简记为1)，并允许我们自由选择结算利息的次数。

如果我们存入银行1块钱，那么我们一年最多能够赚多少钱呢？

(1) 如果只在年底结算一次利息，由于一年的利率是1，那么一年后我们可以连本带利得到2块钱。

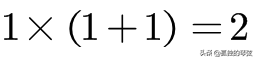
(2) 如果我们要求每半年就结算一次利息，由于半年的利率是1/2，那么一年后我们可以连本带利得到2.25块钱。

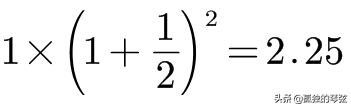
(3) 如果我们要求每一个月就结算一次利息，由于一个月的利率是1/12，那么一年后我们可以连本带利得到2.61块钱。

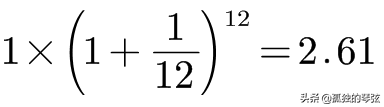
(4) 可以看到，利息结算次数越多，年底获得的收入也就越多。

如果我们脑洞大开，要求银行时时刻刻为我们结算利息，也就是说结算利息的次数为无数次，那么我们能否得到无穷无尽的收入，实现数钱数到手抽筋的梦想呢？

很遗憾，这个是不可能的！因为我们最终获得的收入其实就是下面这个式子，

而数学家的计算已经表明，这个式子的值其实是有限的，其大小为2.718281828…，是一个无限不循环小数，为了使用方便，我们就用e来代表它。

所以，e就是复利的极限，或者更广义地说，应该是增长的极限。