spss主成分分析步骤是什么（主成分分析怎么做）

一．原始数据的输入

注意事项：关键注意设置好数据的类型（数值？字符串？等等）以及小数点后保留数字的个数即可。

二．选项操作

1. 打开SPSS的“分析”→“降维”→“因子分析”，

打开“因子分析”对话框（如下图）

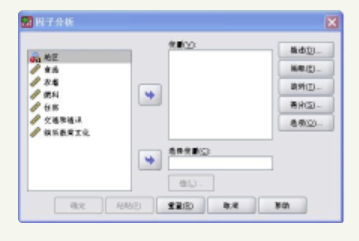
2. 把六个变量：食品、衣着、燃料、住房、交通和通讯、娱乐教育文化输入到右边的待分析变量框。

3. 设置分析的统计量

打开最右上角的“描述”对话框，选中“统计量”里面的“原始分析结果”和“相关矩阵”里面的“系数”。（选中原始分析结果，SPSS自动把原始数据标准差标准化，但不显示出来；选中系数，会显示相关系数矩阵。）。然后点击“继续”。

打开第二个的“抽取”对话框：“方法”里选取“主成分”；“分析”、“输出”和“抽取”这三项都选中各自的第一个选项即可。然后点击“继续”。

第三个的“旋转”对话框里，选取默认的也是第一个选项“无”。

第四个“得分”对话框中，选中“保存为变量”的“回归”；以及“显示因子得分系数矩阵”。

第五个“选项”对话框，默认即可。

这时点击“确定”，进行主成分分析。

三．分析结果的解读

按照SPSS输出结果的先后顺序逐个介绍

1.相关系数矩阵：是6个变量两两之间相关系数大小的方阵。

2.共同度：

给出了这次主成分分析从原始变量中提取的信息，可以看出交通和通讯最

3.总方差的解释：

系统默认方差大于1的为主成分，所以只取前两个，前两个主成分累加占到总方差的80.939%。并且第一主成分的方差是3.568，第二主成分的方差是1.288。

4. 主成分载荷矩阵：

应该特别注意：

这个主成分载荷矩阵并不是主成分的特征向量，也就是说并不是主成分1和主成分2的系数，主成分系数的求法是：各自主成分载荷向量除以各自主成分特征值的算术平方根。那么第1主成分的各个系数是向量（0.925, 0.902, 0.880, 0.878, 0.588, 0.093）除以.568后得到，即(0.490, 0.478, 0.466, 0.465, 0.311, 0.049)（这才是主成分1的特征向量，满足条件：系数的平方和等于1），分别乘以6个原始变量标准化之后的变量即为第1主成分的函数表达式：

Y1?0.490*Z交?0.478*Z食?0.466*Z衣?0.465*Z住?0.311*Z娱?0.049*Z燃

同理可以求出第2主成分的函数表达式。（同学们自己求解！）

5. 主成分得分系数矩阵

该矩阵是主成分载荷矩阵除以各自的方差得来的，实际上是因子分析中各个因子的系数，在主成分分析中可以不考虑它。

6. 因子得分

在步骤二中，第四个“得分”对话框中，我们选中“保存为变量”的“回归”；以及“显示因子得分系数矩阵”。SPSS的输出结果和原始数据一起显示在数据窗口里面：

特别提醒：

后两列的数据是北京等16个地区的因子1和因子2的得分，不是主成分1和主成分2的得分。主成分的得分是相应的因子得分乘以相应的方差的算术平方根。即：主成分1得分=因子1得分乘以3.568的算术平方根

主成分2得分=因子2得分乘以1.288的算术平方根

四．主成分的得分：

把因子1和因子2的数值分别乘以各自的方差的算术平方根，得出各地区主成分1和主成分2的得分。

后两列就是这16个地区主成分1和主成分2的得分。

（有兴趣的同学可以验证一下：由步骤3.4推导出来的主成分的函数关系式计算出来的主成分得分是否与该数据栏的得分一致？）

五．综合得分及排序：

每个地区的综合得分是按照下列公式计算的：

3.5681.288Y?*主成分1得分?*主成分2得分， 化简得： 3.568?1.2883.568?1.288

Y?0.7348*主成分1得分?0.2652*主成分2得分。

按照此公式计算出各地区的综合得分Y为：

按照综合得分Y的大小进行16个地区的排序，结果如下： 9

特别提醒：

1. 如果主成分分析中有n个变量，则特征值（或方差）之和就等于n。

2. 特征向量（或主成分的系数）中各个数值的平方和等于1，否则就不是特征

向量，也不是主成分系数。

3. 步骤3.4中的主成分载荷向量各系数的平方和等于其对应的主成分的方差。

在本例中：0.9252?0.9022?0.8802?0.8782?0.5882?0.0932?3.568

4. SPSS没有专门的主成分分析模块，是在因子分析模块进行的。它只输出主成

分载荷矩阵和因子得分值，而我们最想得到的主成分的系数（特征向量）和主成分得分则需要另外计算。

5. 如果计算没有错误，因子1、因子2、主成分1、主成分2和综合得分Y，它

们各自的数值之和都等于0。

6. 主成分分析应该计算出综合得分并排序。